Duo Fitting¶
Duo allows the user to modify (refine) the potential energy curves and other coupling curves by least-squares-fit to experimental energy term values or wavenumbers.
Duo uses Gauss-Newton least-squares fitting supplemented with the Marquardt approach.
Optionally, this algorythm can be supplemented
by a linear search via the keyword linear-search. The associated system of linear equations
is solved either using the LAPACK subroutine DGELSS or a home-made subroutine LINUR
as controlled by the keyword FIT_TYPE.
Fitting is, by far, the trickiest part of Duo, both on the part of the program itself and on the part of the user. While the calculation of energy levels and spectra from given PECs, couplings and dipole curves is relatively straighforward (the most critical point being the consistency of the phases specified for the various coupling terms), fitting is often more difficult and may require a trial-and-error approach. Fitting is also the part of Duo where most improvements are to be expected in future new versions.
Example of a fitting section:
FITTING
JLIST 2.5,0.5, 1.5 - 11.5, 22.5 - 112.5
itmax 30
fit_factor 1e6
output alo_01
fit_type dgelss
fit_scale 0.001
linear_search 5
lock 5.0
robust 0.001
energies (J parity NN energy ) (e-state v ilambda isigma omega weight)
0.5 + 1 0.0000 1 0 0 0.5 0.5 100.000
0.5 + 2 965.4519 1 1 0 0.5 0.5 7.071
0.5 + 3 1916.8596 1 2 0 0.5 0.5 5.774
0.5 + 4 2854.2366 1 3 0 0.5 0.5 5.000
0.5 + 5 3777.5016 1 4 0 0.5 0.5 4.472
0.5 + 6 4686.7136 1 5 0 0.5 0.5 4.082
0.5 + 7 5346.1146 2 0 1 -0.5 0.5 100.000
end
When state labels are used as potential IDs, i.e.
potential X
......
...
end
potential A
......
...
end
The same labels must be used to identify the electronic states in the energy part of the FITTING section:
FITTING
JLIST 2.5,0.5, 1.5 - 11.5, 22.5 - 112.5
itmax 30
fit_factor 1e6
lock 5.0
energies (J parity NN energy ) (e-state v ilambda isigma omega weight)
0.5 + 1 0.0000 X 0 0 0.5 0.5 100.000
0.5 + 2 965.4519 X 1 0 0.5 0.5 7.071
0.5 + 3 1916.8596 X 2 0 0.5 0.5 5.774
0.5 + 6 4686.7136 X 5 0 0.5 0.5 4.082
0.5 + 7 5346.1146 A 0 1 -0.5 0.5 100.000
end
Fitting ranges¶
The fitting ranges can be proved to set bound for the fittnig parameters as follows:
poten Ap
name "Ap2Delta"
lambda 2
mult 2
type EHH
values
V0 1.47076002476226e+04 fit
RE 1.81413234392416e+00 fit range 1.7,1.9
DE 5.92200000000000E+04 link 1,2,3
ALPHA 1.51288898501269E+00 fit
C 6.54666674267795E-03 fit
B1 -2.63874034064552E+00 fit
B2 -4.80709545680641E+00 fit
B3 0.000000000000000000
end
where the keyword range is followed by the corresponding bound for the corresponding parameter (using the same units). The keyword range and fit are complementary. The input is not sensitive to their order, as long they appear after column 2.
These bound will prevent the varying parameter 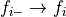 at the iteration
at the iteration 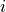 to get a value outside its bounds by applying the following conditions:
.. math:
to get a value outside its bounds by applying the following conditions:
.. math:
\begin{split}
f_{i} &= \max(f_{i-1},f_{\rm min} ) \\
f_{i} &= \min(f_{i-1},f_{\rm max} ) \\
\end{split}
where 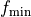 and
and 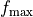 are the corresponding bounds.
are the corresponding bounds.
Keywords¶
FITTING
This keyword marks the beginning of the fitting input section. The whole section
can be deactivated by putting none or off next to the keyword FITTING. This is useful to disable the fitting
without removing the input block from the input file.
jlist(aliases arejrotandJ)
This keyword allows the user to specify the values of the 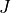 quantum number to be used in the fit.
It superseedes the corresponding
quantum number to be used in the fit.
It superseedes the corresponding jrot keyword specified in the general setup
Individual values of 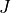 can be separated by spaces or commas, while ranges are specified by two values separated by a hyphen
(hyphens should be surrounded by spaces). The first
can be separated by spaces or commas, while ranges are specified by two values separated by a hyphen
(hyphens should be surrounded by spaces). The first 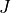 value is used to determine ZPE. For example
value is used to determine ZPE. For example
JLIST 1.5, 5.5, 15.5 - 25.5, 112.5
selects the values 1.5, 5.5, all values from 15.5 to 25.5 and the value 112.5.
itmax(aliasitermax) An integer defining the maximum number of fitting iterations.
Setting itmax to zero implies that no fit will be performed (straight-through calculation); however, the differences between
the computed energy levels (or frequencies) and the reference (experimental) ones will be printed.
Example:
itmax 15
fit_factorThis factor is used when reference curves of theabinitiotype are included in the fit and used to define the importance of the energy/frequency data relative to the referenceabinitiodata. This factor is applied to all energy (frequencies) weight factors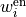 .
.
When the factor is very large (e.g. 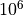 , like in the example above) the penalty for deviating from the reference ‘ab initio’ curve is very small, so that only the obs. - calc. for energy levels matter. Vice versa, if the factor is very small (e.g.
, like in the example above) the penalty for deviating from the reference ‘ab initio’ curve is very small, so that only the obs. - calc. for energy levels matter. Vice versa, if the factor is very small (e.g. 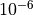 ) the fit is constrained so that the fitted
curves stay very close to the reference (
) the fit is constrained so that the fitted
curves stay very close to the reference (abinitio) ones. When this number is extremely small (smaller than 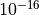 )
the experimental data are completely ignored and the fit is performed to the aivalues only. Thus this feature also allows one to use the
)
the experimental data are completely ignored and the fit is performed to the aivalues only. Thus this feature also allows one to use the FITTING section for building analytical representations (see type-s currently available) of different objects by fitting to the corresponding aior reference data provided in the abinitio-sections of the input.
Example:
fit_factor 1e2
Lock,``Thresh_Assign``
Lock or Thresh_Assign denotes the threshold (cm-1) for which the quantum numbers are used to match to the experimental
value and to lock during the refinement. The quantum numbers defining state,  ,
, 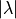 ,
, 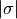 and
and  will be used to identify, match and lock the energy value in place of the running number within the
will be used to identify, match and lock the energy value in place of the running number within the 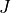 /parity block.
When
/parity block.
When Lock is zero or not present, this feature is switched off and the running number is used to match the experimental and calculated values.
When negative, the match is reconstructed based solely on the closest value within the lock-threshold given.
If the match within the lock-region is not found, the row 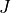 /parity number is used to match the theoretical
and experimental energies. For example to match and lock to the calculated energy to the experimental one based
on the quantum numbers within 20 cm-1 use:
/parity number is used to match the theoretical
and experimental energies. For example to match and lock to the calculated energy to the experimental one based
on the quantum numbers within 20 cm-1 use:
lock 20.0
thresh_obs-calcThis keywords triggers switching off states from the fit if the obs.-calc. residuals become larger than the threshold specified.
This feature is useful in case of multiple swapping of the states during the fits and even the lock option does not help. The default value is zero (the feature is off).
rangeThis keyword is to specify the fitting bounds for a given fitting parameter and should appear on the same line as the parameter value, normally after the keywordfit:
poten Ap
.....
....
values
V0 1.47076002476226e+04 fit
RE 1.81413234392416e+00 fit range 1.7,1.9
......
end
robustThis keyword allows the user to switch on
Watson’s robust fitting procedure: 0 is off, any other positive value
is on and defines the target accuracy of the fit as given by the weighted root-mean-square
error. The robust-value is the targeted accuracy (obs.-calc.) of the fit.
Example:
robust 0.01
target_rms
This is to define the convergence threshold (cm-1) for the total, not-weighted root-mean-squares (rms) fitting error. Example:
target_rms 0.1
output
This is the filename for the files name.en, name.freq and name.pot, containing detailed information on the fitting, including the fitting residuals for each iteration. Example:
output NaH_fit
linear_search
When the linear_search (Damped Gauss-Newton) keyword is given and the associated value integer value is not zero,
Duo will attempt a linear search of the scaling factor 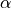 for the
correction parameter vector
for the
correction parameter vector 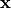 :
:
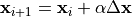 ,
,
where 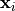 is the paramor vector for the iteration
is the paramor vector for the iteration 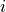 ,
, 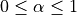 ,
,
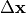 is the least-squares correction. The step length
is the least-squares correction. The step length 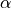 needs to
satisfy the Armijo condition. The keywords
needs to
satisfy the Armijo condition. The keywords linear_search comes with an integer parameter 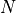 defining the maximal number of
steps in the linear search staring from
defining the maximal number of
steps in the linear search staring from 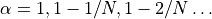 .
Example:
.
Example:
linear_search 5
fit_type
There are two linear solvers available to solve the linear systems associated with
the noon-linear squares fit using Gauss-Newton, fit_type LINUR (home made solver)
and fit_type DGELSS (LAPACK). The latter should be more stable for strongly correlated
systems while LINUR is usually with faster convergence, but for most cases these two methods
should be equivalent.
fit_scale
This is fixed-value analogy of the linear scaling. It directly defies a scaling factor 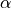 used
to scale the parameter vectors increment :math:Delta {bf x}`, see above. It is ignored when
used
to scale the parameter vectors increment :math:Delta {bf x}`, see above. It is ignored when linear_scaling is
defined. It can be used to improve the convergence.
Example:
fit_scale 0.5
energies
This keyword starts the section with the energy levels to be fit to (e.g., obtained from an analysis of the experimental line positions). Energy levels are written as in the following example:
energies
0.5 + 1 0.0000 1 0 0 0.5 0.5 1.00
0.5 + 2 965.4519 1 1 0 0.5 0.5 0.90
0.5 + 3 1916.8596 1 2 0 0.5 0.5 0.80
end
where the meaning of the various quantities is as follows; col.1 is the total angular momentum quantum number 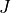 ;
;
col. 2 either the total parity 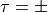 or the
or the 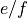 parity;
parity;
col. 3 is a running number 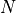 couting levels in ascending order of the energy within a
couting levels in ascending order of the energy within a 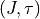 symmetry block;
symmetry block;
col. 4 is the energy term value 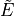 , in cm-1;
, in cm-1;
col. 5 is the electronic state index state, as labelled in the potential sections, e.g. 1 or X;
col. 6 is the vibrational quantum number  ;
;
col. 7 is the projection of the electronic angular momentum 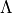 for the state in question (an integer); only the absolute value is used to match to the calculated value;
for the state in question (an integer); only the absolute value is used to match to the calculated value;
col. 8 is the projection of the total electronic spin 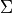 (integer of half integer); only the absolute value is used to match to the calculated value;
(integer of half integer); only the absolute value is used to match to the calculated value;
col. 9 is the projection of the total angular momentum 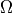 (integer of half integer); only the absolute value is used to match to the calculated value;
(integer of half integer); only the absolute value is used to match to the calculated value;
col. 10 is the weight 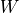 of the experimental energy in question (a real and positive number usually given by
of the experimental energy in question (a real and positive number usually given by 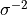 , where
, where 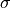 is the uncertainty of the energy level).
is the uncertainty of the energy level).
frequency(aliases arefrequenciesandwavenumbers)
This keyword works similarly to the energies keyword above but starts the section specifying the wavenumbers (i.e., line positions) to be fitted to.
Example:
frequencies
0.0 + 2 0.0 + 1 720.0000 2 0 1 -1.0 0.5 1 0 0 0.0 0.0 1.00
2.0 + 17 3.0 - 2 5638.1376 4 0 0 1.0 1.0 2 0 -1 -1.0 -2.0 1.00
4.0 + 17 5.0 - 2 5627.5270 4 0 0 1.0 1.0 2 0 -1 -1.0 -2.0 1.00
4.0 + 18 7.0 - 2 5616.7976 4 0 0 0.0 0.0 2 0 -1 -1.0 -2.0 1.00
end
The meaning of the quantities in each line are the following (see the keyword energies
above for an explanation of the symbols. The prime/double prime symbol correspond to upper/lower level):
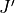 ,
, 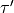 ,
, 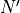 ,
, 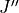 ,
, 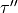 ,
, 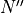 ; frequency (cm-1);
state
; frequency (cm-1);
state ,
, 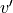 ,
, 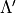 ,
, 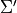 ,
, 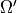 ; state
; state ,
, 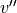 ,
,
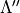 ,
, 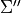 ,
, 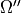 ; weight.
; weight.
off,noneare used to switch offFitting,IntensityorOverlap, when put next to these keywords.
Structure of the fitting output¶
During fitting Duo will print for each iterations the fitting residuals using the following structure (the first line with numbers 1 to 20 is not part of the output but serves as a legend):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1 0.5 + 0.0000 0.0000 0.0000 0.60E-02 1 0 1 -0.5 0.5 0.5 1 0 1 -0.5 0.5 0.5
2 2 0.5 + 1970.2743 1970.3983 -0.1240 0.59E-02 1 1 1 -0.5 0.5 0.5 1 1 1 -0.5 0.5 0.5
3 3 0.5 + 3869.6639 3869.7934 -0.1295 0.30E-02 1 2 1 -0.5 0.5 0.5 1 2 1 -0.5 0.5 0.5
4 4 0.5 + 5698.7392 5699.2951 -0.5559 0.20E-02 1 3 1 -0.5 0.5 0.5 1 3 1 -0.5 0.5 0.5
5 1 0.5 - 0.1001 0.0000 0.1001 0.60E-02 1 0 -1 0.5 -0.5 0.5 1 0 -1 0.5 -0.5 0.5
6 2 0.5 - 1970.4156 1970.3983 0.0173 0.59E-02 1 1 -1 0.5 -0.5 0.5 1 1 -1 0.5 -0.5 0.5
The meaning of the quantities in the various columns is as follows;
col.1 is a simple line counter 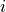 counting over all lines;
counting over all lines;
col.2 is a counter 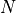 counting lines within each
counting lines within each 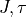 symmetry block;
symmetry block;
col. 3 is 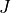 ; col. 4 is the parity
; col. 4 is the parity 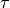 ;
;
col.5,6 are, respetively, the reference (Observed) and the calculated value of the line position;
col.7 is the difference between observed and computed line positions;
col. 8 is the weight assigned to the transition in the fit;
col. 9 to 14 are the quantum numbers of the lower state: state,  ,
, 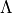 ,
, 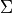 ,
, 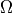 and
and 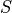 ;
;
col. 15 to 20 are the quantum numbers for the upper state (same definition as for columns 9 to 14).
The auxiliary files .en, .freq, .pot
The files name.en contains all computed term values together with the theoretical quantum numbers, compared to the experimental
values, when available, along with the experimental quantum numbers as specified in the
fitting section, for all iterations of the least-squares fit. Here name
is the file name as speficied by the output keyword. The output is in the same format as in the
standard output file (see above) with the difference that it contains all calculated
values (subject of the nroots keyword, see Section ref{s:diagonaliser}). An
asterisk * at the end of the line indicates that either the theoretical and
experimental assignments don’t agree or a residuals obs.-calc. is too large (large than
the lock parameter).
The frequency file name.freq with the keyword
frequencies. It has a similar structure as the standard output, with the
difference that for each transition from the frequency section the program will
estimate additional transition frequencies involving energies (both lower and
upper) which are within lock cm-1 of the corresponding input values. This is done
to facilitate the search for possible miss-assignment, which is typical for transitions.
This is printed out for all iterations.
The file {name.pot (potential) contains the
residuals between the fitted and the reference
curve (if specified by an abinitio object).
The file is overwritten at each iteration.
Fitting grid points¶
Although usually the fitted object has to be represented in some parameterised functional with the parameters varied in a least-squares fit. It is however also possible to vary grid values of a field in the grid representation. The idea behind this approach is based on the fact that Duo uses cubic splines when mapping a (usually smaller) grid (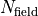 ) of values given in the input to the (usually larger) Duo grid of points
) of values given in the input to the (usually larger) Duo grid of points 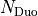 . In principle, the functional values
. In principle, the functional values 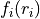 can be treated as parameters defining the function
can be treated as parameters defining the function 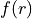 via its values at the corresponding grid points
via its values at the corresponding grid points 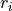 (
(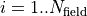 ) via the cubic splines. This works especially well for a very small number of points
) via the cubic splines. This works especially well for a very small number of points 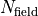 . In Duo input is very analogous to the standard parameterised fit via the keyword
. In Duo input is very analogous to the standard parameterised fit via the keyword fit after the parameter values, for example
spin-orbit 1 1
name "<X2Delta|SO|X2Delta>"
spin 0.5 0.5
lambda 2 2
sigma 0.5 0.5
type grid
factor 1.0 (sqrt2)
values
0.750000000000 -597.1915000 fit
1.200000000000 -590.2260000 fit
1.500000000000 -599.7850000 fit
2.000000000000 -603.9980000 fit
3.000000000000 -603.0000000 fit
end
Constrained fit to ab initio¶
If abinitio fields are provided, the is automatically constrained to the ab initio values of a given field. This can be useful, when the number of experimental data is very limited in order to be able all the parameters required to represent the full complexity of the fitted function. This is implemented as a simultaneous of the same parameters both to the experimental energies (frequencies) and to the ab initio values. In this case it is necessary to control the relative importance of the experimental and the ab initio data using the keyword fit_factor in the fitting section, for example:
::
FITTING JLIST 2.5,0.5, 1.5 - 11.5, 22.5 - 112.5 itmax 30 fit_factor 1e6 …..
The (real) value of fit_factor  is a factor used to scale the experimental fitting weights
is a factor used to scale the experimental fitting weights 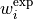 . The ab initio weight factors can be also scale individually also using the keyword
. The ab initio weight factors can be also scale individually also using the keyword fit_factor placed in the corresponding ``abinitio field, for example:
abinitio poten X
name "X2Sigma"
lambda 0
symmetry +
mult 2
fit_factor 0.001
type grid
values
1.400000 40782.9118
1.450000 28672.6462
....
end
As described in the section about the fitting keywords, when the ‘experimental’ fit_factor is very large (e.g. 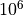 ) the penalty for
deviating from the
) the penalty for
deviating from the `abinitio` (reference) curve is very small, so that only the `obs. - calc.` for energy levels matter.
Vice versa, if the experimental factor is very small (e.g. :math:`10^{-6}`) or if the '*ab initio*' ``fit_factor is very larger, the fit favours the reference (abinitio) data. When this experimental fit_factor is extremely small (smaller than 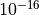 ) the experimental data are completely ignored and the fit is performed to the ab initio values only. Thus this feature also allows one to use the
) the experimental data are completely ignored and the fit is performed to the ab initio values only. Thus this feature also allows one to use the FITTING section for building analytical representations (see type-s currently available) of different objects by fitting to the corresponding aior reference data provided in the abinitio-sections of the input.
It should be noted that the reference (abinitio) curve does not have to be a grid field. Any representation, including analytic ones cane be used to constrained the varying parameters to a reference field.
Ab initio weights¶
For the constrained fit to work, the ab initio data must be weighted. This is done by adding a column 3 with the corresponding weights, e.g. :
abinitio poten X
name "X2Sigma"
lambda 0
symmetry +
mult 2
type grid
fit_factor 0.1
values
1.400000 40782.9118 0.5
1.450000 28672.6462 0.6
1.500000 19310.0950 0.7
1.550000 12244.8264 0.8
1.600000 7101.7478 0.9
1.650000 3562.3190 1.0
Alternatively, the weights can be also defined using the WEIGHTING keyword, with a predefined weight function PS1997 for 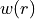 according with the weighting form suggested by Partridge and Schwenke (1997):
according with the weighting form suggested by Partridge and Schwenke (1997):
![w(r) = \tanh(-\beta [(V(r) - V_{\rm min}) - V_{\rm top}] + 1.000020000200002 )/2.000020000200002](_images/math/18a22c45af2bf53cf7f5aadf51e754a9094cfb6e.png)
where 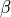 and
and 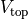 are weighting parameters and
are weighting parameters and 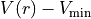 is the potential function of the corresponding field, shifted to zero.
is the potential function of the corresponding field, shifted to zero.
For example, a weighting function of a potential field can be given by
abinitio poten 1 name "X 2Pi"
lambda 1
mult 2
type grid
Weighting PS1997 1e-3 20000.0
fit_factor 1e-8
values
0.6 610516.16994 0
0.7 294361.15182 0
Here 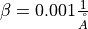 and
and 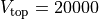 cm-1.
cm-1.
The Weighting feature can be used for couplings as well. In this case the values of 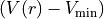 are taken from the potential that corresponds to the coupling in question. Here is an example for a diagonal spin-orbit field:
are taken from the potential that corresponds to the coupling in question. Here is an example for a diagonal spin-orbit field:
abinitio spin-orbit-x A A
name "<A2Pi|LSZ|A2Pi>"
spin 0.5 0.5
lambda 1 1
sigma 0.5 0.5
factor -i 1.175
fit_factor 1e-2
weighting ps1997 0.0001 45000.0
type grid
<x|Lz|y> -i -i
values
1.58 163.05
1.59 163.82
....
end
For a non-diagonal coupling between 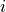 and
and 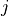 states, Duo will use the potential corresponding to the first index
states, Duo will use the potential corresponding to the first index 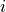 to define
to define 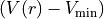 to calculate the weights according with the equation above.
to calculate the weights according with the equation above.
Example: Refinement of the BeH PEC curve¶
This PEC can be refined by fitting to experimental energies using the following input structure:
poten 1
name 'X2Sigma+'
lambda 0
symmetry +
mult 2
type EMO
Values
V0 0.00
RE 1.342394
DE 17590.00 fit
RREF -1.00000000
PL 3.00000000
PR 3.00000000
NL 0.00000000
NR 0.00000000
b0 1.8450002 fit
end
FITTING
JLIST 0.5 - 0.5
itmax 12
fit_factor 1e5
output BeH_01
lock 1000
robust 0.0001
energies ( state v ilambda isigma omega weight comment <- state v ilambda isigma weigh
0.5 + 1 0 1 0 0 0.5 0.5 1.00
0.5 + 2 1986.416 1 1 0 0.5 0.5 1.00
0.5 + 3 3896.871 1 2 0 0.5 0.5 1.00
0.5 + 4 5729.26 1 3 0 0.5 0.5 1.00
0.5 + 5 7480.338 1 4 0 0.5 0.5 1.00
0.5 + 6 9145.132 1 5 0 0.5 0.5 0.00
0.5 + 7 10716.163 1 6 0 0.5 0.5 0.00
0.5 + 8 12182.207 1 7 0 0.5 0.5 0.00
0.5 + 9 13525.788 1 8 0 0.5 0.5 0.00
0.5 + 10 14718.082 1 9 0 0.5 0.5 0.00
0.5 + 11 15709.384 1 10 0 0.5 0.5 0.00
end
The ab initio potential energy curve can be kept to control the shape of the refined curve:
abinitio poten 1
units cm-1 angstroms
name 'X2Sigma+'
lambda 0
symmetry +
mult 2
type grid
values
0.60 105169.63
0.65 77543.34
0.70 55670.88
0.75 38357.64
0.80 24675.42
0.85 13896.77
0.90 5447.96
0.95 -1125.87
1.00 -6186.94
1.05 -10024.96
1.10 -12872.63
1.15 -14917.62
1.20 -16311.92
1.25 -17179.13
1.30 -17620.16
1.32 -17696.29
1.33 -17715.26
1.34 -17722.22
1.35 -17717.69
1.36 -17702.19
1.37 -17676.19
1.38 -17640.16
1.40 -17539.76
1.45 -17142.53
1.50 -16572.59
1.55 -15868.72
1.60 -15063.34
1.65 -14183.71
1.70 -13252.86
1.80 -11313.
1.90 -9369.74
2.00 -7518.32
2.10 -5832.29
2.20 -4366.71
2.30 -3155.94
2.40 -2208.98
2.50 -1507.72
2.60 -1013.23
2.80 -456.87
3.00 -221.85
3.50 -72.13
4.00 -41.65
4.50 -24.9
5.00 -14.32
6.00 -4.74
8.00 -0.75
10.00 -0.19
20.00 0.0
end