Duo Functions¶
This section shows examples of the definitions of the analytical functions supported in Duo.
Potential energy funcitons¶
Extended Morse Oscillator EMO¶
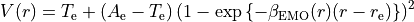 ,
,
which has the form of a Morse potential with a exponential tail and the distance-dependent exponent coefficient
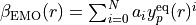 ,
,
expressed as a simple power series in the reduced variable:
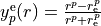
with 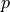 as a parameter. This form guarantees the correct dissociation limit and allows
for extra flexibility in the degree of the polynomial on the left or on the right sides
of a reference position
as a parameter. This form guarantees the correct dissociation limit and allows
for extra flexibility in the degree of the polynomial on the left or on the right sides
of a reference position 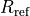 which we take at
which we take at 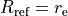 . This is
specified by the parameters
. This is
specified by the parameters 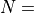
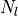 (
(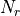 ) and
) and 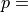
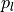 (
(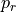 ),
respectively.
),
respectively.
Example:
poten 2
name "a 3Piu"
symmetry u
type EMO
lambda 1
mult 3
values
Te 0.81769829519421E+03
Re 0.13115676812526E+01
Ae 0.50960000000000E+05
RREF -0.10000000000000E+01
PL 4
PR 4
NL 2
NR 3
a0 0.21868146887665E+01
a1 0.88875855351916E-01
a2 0.84932592800179E-01
a3 0.23343175838290E+00
end
Taylor expansion around 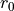 :
:
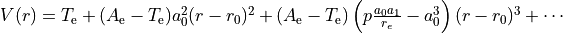
Morse Long-Range (MLR) function MLR¶
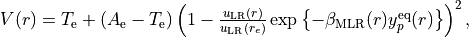
where the radial variable 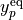 in the exponent, the long-range potential
in the exponent, the long-range potential 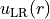 by
by
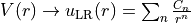 while the exponent coefficient function
while the exponent coefficient function
![\beta_{\rm MLR}(r) = y_p^{\rm{ref}}(r)\, \beta_{\infty} + \left[1 -y_p^{\textrm{ref}}(r)\right] \sum_{i=0} a_i[y_q^{\textrm{ref}}(r)]^i](_images/math/aceee807e89ff6672ea54e2f3ab326b133a039d7.png)
is defined in terms of two radial variables which are similar to 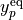 ,
but are defined with respect to a different expansion center
r_textrm{ref}, and involve two different powers,
,
but are defined with respect to a different expansion center
r_textrm{ref}, and involve two different powers, 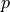 and
and 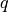 . The above
definition of the function
. The above
definition of the function 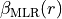 means that:
means that:
![\beta_{\rm MLR}(r\to\infty) \equiv \beta_{\infty} = \ln[2D_{\rm e}/u_{\textrm{LR}}(r_{\rm e})].](_images/math/c7948f3dd437cd732ef5d3c93588cfaf62c60dfb.png)
Example:
poten 6
name "d 3Pig"
symmetry g
lambda 1
mult 3
type MLR
values
Te 0.20151357236994E+05
RE 0.12398935933004E+01
AE 0.50960000000000E+05 link 1 1 3
RREF -0.10000000000000E+01
P 0.40000000000000E+01
NL 0.20000000000000E+01
NR 0.80000000000000E+01
b0 0.30652655627150E+01
b1 -0.93393246763924E+00
b2 0.45686541184906E+01
b3 -0.37637923145046E+01
b4 -0.41028177891391E+01
b5 0.00000000000000E+00
b6 0.00000000000000E+00
b7 0.00000000000000E+00
b8 0.00000000000000E+00
a1 0.00000000000000E+00
a2 0.00000000000000E+00
a3 0.00000000000000E+00
a4 0.00000000000000E+00
a5 0.00000000000000E+00
a6 192774.
a7 0.00000000000000E+00
a8 0.00000000000000E+00
end
Coxon and Hajigeorgiou’s MLR3 Morse Long-Range with Douketis Damping MLR_3¶
The MLR3 potential function is described by Coxon and Hajigeorgiou, JCP 132 (2010) - an adapted form of the standard MLR potential with an additional parameter  in the radial variable
in the radial variable 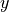 . The form of the potential is given by:
. The form of the potential is given by:
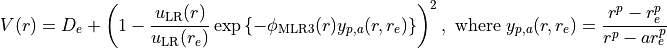
and the the long-range potential function is given by:
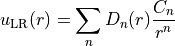
Here Duo uses the generalised Douketis damping functions, defined as:
![D_n(r) = \left(1 - \exp \left[ - \frac{b(s) (\rho r)}{n} - \frac{c(s) (\rho r)^2}{\sqrt{n}} \right] \right)^{m+s}](_images/math/ec2c2f6e72ab8bffcca2890326f11a7ef8682acd.png)
with 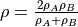 where
where 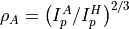 and
and 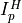 is the ionisation potential of the hydrogen atom.
The
is the ionisation potential of the hydrogen atom.
The 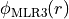 function is given by:
function is given by:
![\phi_\text{MLR3} (r) = y_m(r, r_\text{ref}) \phi_\text{MLR3} (\infty) + \left[ 1 - y_m(r, r_\text{ref}) \right] \sum_{i=0}^{N_\phi} \phi_i y_q(r, r_\text{ref})^i](_images/math/2b6e6c56e4fd1a2101d4df5dba9e20c5818b7845.png)
where
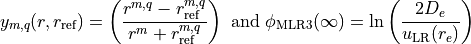
where  is some expansion centre, usually
is some expansion centre, usually 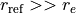 .
.
Most parameters in the input file have a one-to-one correspondence with those in the above equations. The parameter V0 can be set greater than zero if the dissociation energy, 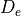 is not defined relative to the potential minimum (i.e
is not defined relative to the potential minimum (i.e 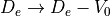 ).
).
Further parameters that do not have obvious definitions are NPWRS and NPHIS. The former specifies the number of inverse power terms to include in the long-range function, and is followed by the order of each power term (in the example below, the first power term is 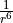 , the second is
, the second is 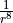 , etc.), the coefficients
, etc.), the coefficients 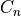 are then specified (
are then specified (COEF1, COEF2, etc.). The parameter NPHIS specifies the number of 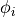 terms to include in the exponent function, and is followed by a list of their values.
terms to include in the exponent function, and is followed by a list of their values.
An example input is given below for HF molecule. The parameters are taken from `Coxon & Hajigeorgiou, JQSRT 151, 133-154 (2015) <https://doi.org/10.1016/j.jqsrt.2014.08.028>.`_
poten 1
name "X1Sigma+"
symmetry +
lambda 0
mult 1
type MLR3
units cm-1 angstroms
values
V0 0.
RE 0.91683897
DE 49361.6
RREF 1.45
P 6
M 11
Q 4
A 150.0
S -0.5
RHO 1.082
B 3.69
C 0.4
NPWRS 3
PWR1 6
PWR2 8
PWR3 10
COEF1 3.1755E+4
COEF2 1.667E+5
COEF3 1.125E+6
NPHIS 32
PHI0 3.54289281000000E+00
PHI1 -5.41984130000000E+00
PHI2 -8.86976500000000E+00
PHI3 -2.93722400000000E+01
PHI4 -4.32900400000000E+01
PHI5 -7.13177000000000E+01
PHI6 -7.77911700000000E+01
PHI7 6.71510000000000E+01
PHI8 -3.51437300000000E+02
PHI9 -4.62131060000000E+03
PHI10 6.72490000000000E+02
PHI11 5.81178370000000E+04
PHI12 1.90159300000000E+04
PHI13 -4.78435670000000E+05
PHI14 -3.29985590000000E+05
PHI15 2.60051860000000E+06
PHI16 2.52642570000000E+06
PHI17 -9.62119030000000E+06
PHI18 -1.17913360000000E+07
PHI19 2.41995750000000E+07
PHI20 3.62543670000000E+07
PHI21 -4.01790300000000E+07
PHI22 -7.51160300000000E+07
PHI23 4.00889000000000E+07
PHI24 1.03908000000000E+08
PHI25 -1.61464000000000E+07
PHI26 -9.20420000000000E+07
PHI27 -9.93600000000000E+06
PHI28 4.71800000000000E+07
PHI29 1.41000000000000E+07
PHI30 -1.06400000000000E+07
PHI31 -4.70000000000000E+06
end
Potential function Marquardt¶
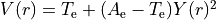 ,
,
which has the form of a Morse potential with a exponential tail and the distance-dependent damped exponent coefficient
:math:` Y(r) left( 1 - expleft{-beta_{rm M}(r) (r-r_{rm e})right} right) f_{rm Damp}(r) `
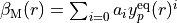 ,
,
expressed as a simple power series in the reduced variable:
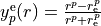
with 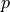 as a parameter. The damping function is give by
as a parameter. The damping function is give by
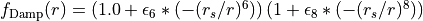
Example:
poten 2
name "a 3Piu"
symmetry u
type Marquardt
lambda 1
mult 3
values
Te 0.81769829519421E+03
Re 0.13115676812526E+01
Ae 0.50960000000000E+05
RREF -0.10000000000000E+01
PL 4
PR 4
NL 2
NR 3
eps6 2.0
eps8 1.0
rs 1.0
a0 0.21868146887665E+01
a1 0.88875855351916E-01
a2 0.84932592800179E-01
a3 0.23343175838290E+00
end
Taylor expansion around 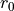 :
:
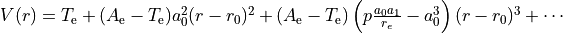
Morse oscillator Morse¶
A polynomial expansion in the Morse variable 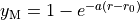 is used
is used
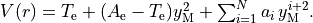
Example
poten 1
name "X 1Sigmag+"
symmetry g +
type MORSE
lambda 0
mult 1
values
TE 0.00000000000000E+00
RE 0.12423216077595E+01
a 0.20372796052933E+01
AE 0.73955889175514E+05
A1 -0.62744302960091E+04
A2 -0.57683579529693E+04
end
Morse_damp¶
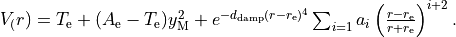
Example:
poten 6
name "d 3Pig"
symmetry g
lambda 1
mult 3
type Morse_damp
values
Te 20121.09769
re 0.12545760270976E+01
Ae 0.50937907750000E+05 link 1 1 3
a0 0.30398932686950E+01
DAMP 0.10000000000000E-02
a1 0.11437702960146E+05
a2 -0.36585731834570E+03
a3 -0.20920472718062E+05
a4 0.90487097982036E-03
a5 0.00000000000000E+00
a6 0.00000000000000E+00
a7 0.00000000000000E+00
a8 0.00000000000000E+00
end
Modified-Morse¶
Alias MMorse
![V_(r)=T_{\rm e}+ (A_{\rm e}-T_{\rm e}) \frac{ \left[ 1-\exp\left(-\sum_{i=0} a_i \xi^{i+1}\right) \right]^2}{\left[ 1-\exp\left(-\sum_{i=0} a_i \right) \right]^2},](_images/math/aeab5f05713fa7ffa2bba3813916e2a3155783c4.png)
where 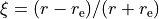 .
.
Example:
poten 8
name "Bp 1Sigmag+"
symmetry g +
lambda 0
mult 1
type MMorse
values
Te 1.5408840263E+04
rE 1.3778208709E+00
Ae 5.0937907750E+04 link 1 1 3
a0 6.2733066935E+00
a1 1.4954972843E+01
a2 4.5160872659E+01
end
where the value 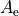 is linked to the corresponding value of
is linked to the corresponding value of poten 1.
Polynomial¶
This keyword selects a polynomial expansion in the variable 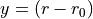
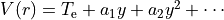
Example:
spin-orbit 2 2
name "<+1,S=1 (a3Pi)|LSZ|+1 (a3Pi),S=1>"
spin 1.0 1.0
sigma 1.0 1.0
lambda 1 1
type polynom
factor 1
values
a0 14.97
re 1.3
a1 0.0
end
Taylor expansion around 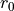 :
:
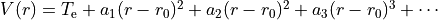
Dunham expansion
Dunham selects a polynomial expansion in the Dunham variable 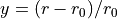
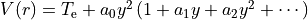
Example:
poten 1
name "X 2 Delta"
lambda 2
mult 2 type Dunham values
Te 0.00000
Re 1.4399282269779912
a0 123727.20496894409 (= omega**2 / 4 B)
a2 -2.31
a3 3.80
a4 -6.00
a5 5.00
end
Taylor expansion around 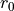 :
:
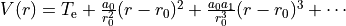
Simons, Parr and Finlan SPF¶
SPF selects a polynomial expansion in the the so-called Simons, Parr and Finlan variable 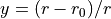
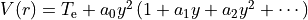
Example:
poten 1
name "X 2Sigma+"
symmetry +
type SPF
lambda 0
mult 2
values
Te 0.00000000000000E+00
RE 0.16292698613903E+01
a1 0.37922070444743E+06
a2 0.00000000000000E+00
a3 -0.53314483965665E+01
a4 0.00000000000000E+00
a5 0.19407192336518E+02
a4 0.00000000000000E+00
a5 -0.17800496953835E+03
end
Taylor expansion around 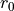 :
:
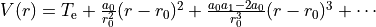
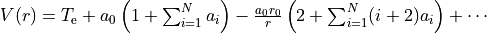
where 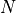 is the maximum exponent included in the expansion.
For long
is the maximum exponent included in the expansion.
For long  the potential goes to a constant value; convergence to the constant
is of the
the potential goes to a constant value; convergence to the constant
is of the 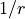 type (correct for ions but too slow for neutral molecules).
type (correct for ions but too slow for neutral molecules).
Behaviour for 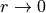
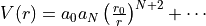
The coefficient 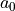 is definitely positive, but
is definitely positive, but 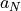 can be positive and negative,
so that
can be positive and negative,
so that 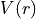 can go to
can go to 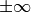 for short
for short  .
.
Murrell-Sorbie M-S¶
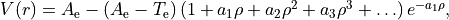 `
where
`
where 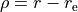 .
.
Example:
poten 4
name "B 2Sigma"
symmetry -
type M-S (Murrell-Sorbie)
lambda 0
mult 2
values
V0 21000.0
RE 1.6
DE 25653.27131
a1 2.81468
a2 1.68719
a3 0.757787
a4 -0.5963168
a5 -0.54596343
a6 0.20611664
end
Taylor expansion around 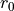 :
:
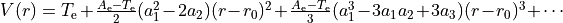
Behaviour for 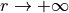 :
:
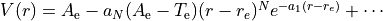 `
where
`
where 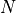 is the maximum exponent included in the expansion.
For long
is the maximum exponent included in the expansion.
For long  the potential goes to the constant value
the potential goes to the constant value 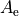 , and the aymptotic behavior is
determined by the coefficients of the term with the highest exponent.
, and the aymptotic behavior is
determined by the coefficients of the term with the highest exponent.
Chebyshev¶
This keyword selects an expansion in Chebyshev polynomials in the variable
![y= [r-(b+a)/2]/[(b-a)/2]](_images/math/54e0ce56743bc2440343f4581db2efd320fd759e.png) . The scaled variable
. The scaled variable 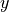 ranges from
ranges from 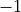 to 1 for
to 1 for  in
in ![[a,b]](_images/math/b17897287b23d96473a85f41eeb859a16830b679.png) . The expansion is
. The expansion is
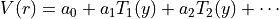
Example:
spin-orbit 2 2
name "<+1,S=1 (a3Pi)|LSZ|+1 (a3Pi),S=1>"
spin 1.0 1.0
type chebyshev
factor 1
values
a 0.80000000000000E+00
b 0.26500000000000E+01
A0 -0.25881057805341E+02
A1 0.82258425882627E+01
A2 0.52391700137878E+00
A3 0.28483394288286E+01
A4 -0.15136422837793E+00
A5 0.97553692867070E-01
A6 -0.25825811071417E+00
A7 -0.69105144347567E-01
A8 -0.44700771508442E-01
A9 0.11793957297111E-01
A10 0.16403055376257E-01
A11 0.92509900186428E-02
A12 0.50789943150707E-02
A13 -0.39439903216016E-03
end
irreg_chebyshev_DMC¶
based on eq.(3) of https://doi.org/10.1016/j.jqsrt.2022.108255
COSH-POLY¶
This function can be used as a coupling for a diabatic representation of potentials characterised by
an avoiding crossing and is given by:
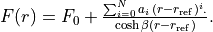
Example
diabatic 1 8
name "<X1Sigmag+|D|Bp 1Sigmag+>"
spin 0.0 0.0
lambda 0 0
type COSH-poly
factor i (0, 1 or i)
values
v0 0.0000
beta 5.62133
RE 1.610505
B0 -0.307997
B1 0.0000000000E+00
B2 0.0000000000E+00
BINF 0.0000000000E+00
end
REPULSIVE¶
A hyperbolic expansion used to represent repulsive potential functions:
:math:`V(r) = sum_{i=0}^N a_0 frac{1}{r^i}.
Example:
poten 2
name "b3Sigmau+"
lambda 0
symmetry + u
mult 3
type REPULSIVE
values
NREP 11
V0 35000
B1 0.00000000000000E+00
B2 0.00000000000000E+00
B3 0.00000000000000E+00
B4 0.00000000000000E+00
B5 0.00000000000000E+00
B6 2.98088692713112e+05 fit
B7 0.00000000000000E+00
B8 0.00000000000000E+00
B9 0.00000000000000E+00
B10 0.00000000000000E+00
end
POLYNOM_DECAY_24¶
This function is similar to Surkus expansion
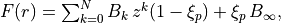
where  is either taken as the damped-coordinate given by:
is either taken as the damped-coordinate given by:
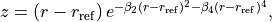
Here  is a reference position equal to
is a reference position equal to 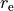 by default and
by default and
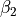 and
and 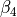 are damping factors.
When used for morphing, the parameter
are damping factors.
When used for morphing, the parameter 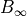 is usually fixed to 1.
is usually fixed to 1.
Example
spin-orbit 6 6
name "<3Pi|LSZ|3Pi>"
spin 1 1
lambda 1 1
sigma 1 1
factor i (0, 1 or i)
<x|LZ|y> -i -i
type polynom_decay_24
morphing
values
RE 1.52
BETA 8.00000000000000E-01
GAMMA 2.00000000000000E-02
P 6.00000000000000E+00
B0 1.000
B1 0.000
B2 0.000
B3 0.00000000000000
BINF 1.0
end
CO_X_UBOS¶
This CO PEC was used in Meshkov et. al, JQSRT, 217, 262 (2017) to compute energies of CO in its ground electronic state. All parameters are predefined internally.
Coupled functions with adiabatic avoided crossings¶
TWO_COUPLED_EMOS¶
This is a combination of two coupled diabatic EMOs coupled with a function given COSH-POLY into adiabatic potentials.
Only one of the two EMOS is requested via the last parameter COMPON.
Example:
poten 1
name "X1Sigmag+"
symmetry g +
type TWO_COUPLED_EMOs
lambda 0
mult 1
N 17
values
V0 0.00000000000000E+00
RE 1.24523246726220e+00 fit ( 1.24557289520164e+00)
DE 5.09379077331962E+04
RREF -1.30000000000000E+00
PL 4.00000000000000E+00
PR 4.00000000000000E+00
NL 1.00000000000000E+00
NR 4.00000000000000E+00
B0 2.46634378637660e+00 fit ( 2.46634099008862e+00)
B1 2.12861537671055e-01 fit ( 2.13213572172644e-01)
B2 3.68744269741852e-01 fit ( 3.67251371602415e-01)
B3 2.79829009743158e-02 fit ( 3.08989242446331e-02)
B4 0.00000000000000E+00
V0 1.53096974359289E+04
RE 1.37782087090000E+00
DE 5.12700000000000E+04
RREF 1.45000000000000E+00
PL 6.00000000000000E+00
PR 6.00000000000000E+00
NL 2.00000000000000E+00
NR 4.00000000000000E+00
B0 1.69821419712600e+00 fit ( 1.69441561141992e+00)
B1 8.82161990201937e-01 fit ( 8.75640185107701e-01)
B2 0.00000000000000E+00
B3 0.00000000000000E+00
B4 0.00000000000000E+00
V0 0.00000000000000E+00
BETA -4.06826947563977E-01
RE 1.61000000000000E+00
B0 1.69000000000000E+03
B1 0.00000000000000E+00
B2 0.00000000000000E+00
COMPON 1.00000000000000E+00
end
COUPLED_EMO_REPULSIVE¶
This is a combination of a EMO and a repulsive diabatic potential coupled by a COSH-POLY function
into adiabatic potentials. Only one of the two adiabatic components is requested via the last parameter COMPON.
Example:
poten 2
name "A1Pi"
lambda 1
mult 1
type COUPLED_EMO_REPULSIVE
values
V0 2.37503864856843e+04 fit ( 2.37512779848526e+04)
RE 1.6483281182 ( 1.73436012667172e+00)
DE 2.84148346146689E+04
RREF -1.00000000000000E+00
PB 4.00000000000000E+00
PU 4.00000000000000E+00
NSPHI 4.00000000000000E+00
NLPHI 4.00000000000000E+00
B0 2.33710099174412e+00 fit ( 2.34057128807870e+00)
B1 0.00000000000000E+00
B2 0.00000000000000E+00
B3 0.00000000000000E+00
B4 0.00000000000000E+00
NREP 1.10000000000000E+01
V0 2.55900000000000E+04
B1 0.00000000000000E+00
B2 0.00000000000000E+00
B3 0.00000000000000E+00
B4 0.00000000000000E+00
B5 0.00000000000000E+00
B6 2.98032773475875e+05 fit ( 2.98032773545535e+05)
B7 0.00000000000000E+00
B8 0.00000000000000E+00
B9 0.00000000000000E+00
B10 0.00000000000000E+00
V0 0.00000000000000E+00
BETA 2.00000000000000E-01
RE 2.20000000000000E+00
B0 9.83507743432739E+02
B1 0.00000000000000E+00
B2 0.00000000000000E+00
COMPON 1.00000000000000E+00
end
TWO_COUPLED_BOBS¶
This form is used to couple two Surkus-like expansion into one adiabatic representation
using two diabatic functions 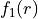 and
and 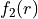 coupled by a switching function. The two diabatic curves
are give by
coupled by a switching function. The two diabatic curves
are give by BobLeroy while the switching function is given by
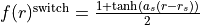
The switch is given by
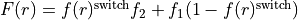
or
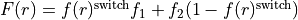
depending on the component requested.
Example:
spin-orbit-x 3 3
name "<A2Pi|LSZ|A2Pi>"
spin 0.5 0.5
lambda 1 1
sigma 0.5 0.5
units cm-1
factor -i (0, 1 or i)
type TWO_COUPLED_BOBS
<x|Lz|y> -i -i
values
RE 1.79280000000000E+00
RREF -1.00000000000000E+00
P 1.00000000000000E+00
NT 2.00000000000000E+00
B0 2.15270130472980E+02
B1 0.0000
B2 0.00000000000000E+00
BINF 190.000
RE 1.79280000000000E+00
RREF -1.00000000000000E+00
P 1.00000000000000E+00
NT 2.00000000000000E+00
B0 -13.000
B1 0.0000
B2 0.00000000000000E+00
BINF 0.00
r0 1.995
a0 100.0
COMPON 1.00000000000000E+00
end
EHH: Extended Hulburt-Hirschfelde¶
This form uis used for PEFs given by
![V^{\rm EHH}(r)=T_{\rm e} + (A_{\rm e}-T_{\rm e}) \left[\left(1-e^{-q}\right)^2 + cq^3\left(1+\sum_{i=1}^N b_i q^i \right) e^{-2q}\right]](_images/math/48a52f03d6a03f5c749c6fd485dabea93ecc1120.png) ,
,
where 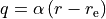 .
See Medvedev and Ushakov J. Quant. Spectrosc. Radiat. Transfer 288, 108255 (2022).
.
See Medvedev and Ushakov J. Quant. Spectrosc. Radiat. Transfer 288, 108255 (2022).
Example:
poten 1
name "X1Sigma+"
symmetry +
lambda 0
mult 1
type EHH
values
TE 0.00000000000000E+00
RE 0.149086580348419329D+01
AE 0.519274276353915047D+05
alpha 0.221879954515301936D+01
c 0.948616297258670499D-01
B1 0.100084121923090996D+01
B2 0.470612349534084318D+00
B3 0.890787339171956738D-01
end
Generic two-state coupled adiabatic potential¶
Any three single functions implemented in Duo can be used to form a coupled 2x2 system to form PEC with avoiding crossings. This is done using the types Coupled-PEC or COUPLED-PEC-BETA, together with sub-types specifying three functions required to form a coupled system, PEC1, PEC2 and Coupling12. This form also requires that the corresponding numbers of parameters are specified using Nparameters. As above, the last parameter is reserved for the component index (1,2) referring to the adiabatic potential. Here is an example of an adiabatic potential with an avoiding crossing formed from a 2x2 ‘diabatic’ system, an EMO potential, a repulsive potential and an (inverted) EMO used as a coupling (from an AlH model):
poten A
name "A1Pi"
lambda 1
mult 1
type coupled
sub-types EMO repulsive EMO
Nparameters 13 12 13
values
V0 2.36706506146433e+04
RE 1.64813484193969e+00
DE 50915.756
RREF -1.00000000000000E+00
PB 4.00000000000000E+00
PU 4.00000000000000E+00
NSPHI 4.00000000000000E+00
NLPHI 4.00000000000000E+00
B0 2.23877956276444e+00
B1 0.000000000000000000
B2 -2.55686572909604e-01
B3 0.00000000000000E+00
B4 0.00000000000000E+00
NREP 11
V0 2.55900000000000E+04
B1 0.00000000000000E+00
B2 0.00000000000000E+00
B3 0.00000000000000E+00
B4 0.00000000000000E+00
B5 0.00000000000000E+00
B6 3.56560923385944e+05
B7 0.00000000000000E+00
B8 0.00000000000000E+00
B9 0.00000000000000E+00
B10 0.00000000000000E+00
V0 6.38813113973348e+03
RE 2.02137412627653e+00
AE 0.000000000000000000
RREF -1.00000000000000E+00
PB 4.00000000000000E+00
PU 4.00000000000000E+00
NSPHI 4.00000000000000E+00
NLPHI 4.00000000000000E+00
B0 1.84063793349509e+00
B1 0.000000000000000000
B2 3.33171505629389e-03
B3 0.00000000000000E+00
B4 0.00000000000000E+00
COMPON 1
end
Here, the keyword sub-type is used to specify the corresponding functions in the form of PEC1 PEC2 COUPLING (COUPLED-PEC) or PEC1 PEC2 BETA (COUPLED-PEC-BETA), where
PEC1, PEC2, COUPLING and BETA are any functions implemented in Duo, e.g. EMO, Lorentzian etc.
In the case of the type COUPLED-PEC, the coupling 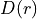 is defined explicitly, while for
is defined explicitly, while for COUPLED-PEC-BETA, it is generated using the transformation angle
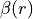 :
:
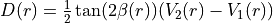 ,
,
where 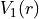 and V_2(r) are PEC1 and PEC2, respectively.
and V_2(r) are PEC1 and PEC2, respectively.
An example of the COUPLED-PEC-BETA input for a potential, produced by the coupling of an EMO, REPULSIVE and a diabatic coupling function 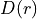 defined via
the
defined via
the 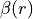 from a Lorentzian form BETA_LORENTZ:
from a Lorentzian form BETA_LORENTZ:
poten A
name "A1Pi"
lambda 1
mult 1
type coupled-pec-beta
sub-types EMO repulsive BETA_LORENTZ
Nparameters 13 12 2
values
V0 2.36706506146433e+04 fit ( 2.36695116221313e+04)
RE 1.64813484193969e+00 fit ( 1.64805055140387e+00)
DE 50915.756
RREF -1.00000000000000E+00
PB 4.00000000000000E+00
PU 4.00000000000000E+00
NSPHI 4.00000000000000E+00
NLPHI 4.00000000000000E+00
B0 2.23877956276444e+00 fit ( 2.23878305838811e+00)
B1 0.000000000000000000 ( 3.41737763224365e-01)
B2 -2.55686572909604e-01 fit ( -2.59129061999807e-01)
B3 0.00000000000000E+00
B4 0.00000000000000E+00
NREP 11
V0 2.55900000000000E+04
B1 0.00000000000000E+00
B2 0.00000000000000E+00
B3 0.00000000000000E+00
B4 0.00000000000000E+00
B5 0.00000000000000E+00
B6 3.56560923385944e+05 fit ( 3.56503862575298e+05)
B7 0.00000000000000E+00
B8 0.00000000000000E+00
B9 0.00000000000000E+00
B10 0.00000000000000E+00
gamma 0.025
RE 2.0452
COMPON 1.00000000000000E+00
end
Here, the first (lowest) component is produced.
Generic two-state coupled adiabatic transition curves (dipoles, spin-orbit, etc)¶
Similarity to the generic COUPLED-PEC-BETA functional form used to represent adiabatic PECs from diabatic functions, COUPLED-TRANSIT-BETA form is used to create non-diagonal adiabatic transition curves (e.g. dipole) from two diabatic curves and a unitary transformation as follows. Here, only one of the two states (bra or ket) describes a coupled 2-state system, another one is assumed a single state. Any two single functions designed for transition and coupling properties implemented in Duo can be used to form such a coupled representation, while the last one should be a function describing the transformation angle 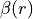 . This form also requires that the corresponding numbers of parameters are specified using
. This form also requires that the corresponding numbers of parameters are specified using Nparameters. As in other similar adiabatic forms,
the last parameter is reserved for the component-index (1,2) referring to the adiabatic state in question. Here is an example of a dipole moment in the adiabatic representation of CH formed from two diabatic bobleroy` DMCs and 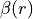 in the form of a Lorentzian-type form
in the form of a Lorentzian-type form BETA_Lorentz:
dipole X C
name "<X2Pi|DMX|C2Sigma>"
spin 0.5 0.5
lambda 1 0
type coupled-transit-beta
sub-types bobleroy bobleroy BETA_Lorentz
Nparameters 7 7 2
values
RE 1.4
RREF -1.00000000000000E+00
P 4
NT 1
B0 0.71
B1 0.09
BINF 0.00000000000000E+00
RE 1.27
RREF -1.00000000000000E+00
P 5
NT 1
B0 0.85
B1 0.17
BINF 0.00000000000000E+00
gamma 0.2
RE 1.6566449350
COMPON 1
end
Here, the first (lowest) component is produced. The keyword sub-type is used to specify the corresponding functions in the form of DMC1 DMC2 BETA, where DMC1, DMC2 and BETA are any functions implemented in Duo, e.g. boblery, beta_Lorentzian etc.
The transformation from 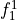 and
and 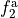 from
from 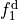 and
and 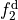 is via the transformation angle
is via the transformation angle 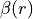 is defined as follows
is defined as follows
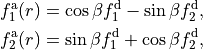
and COMPON =1,2 is to select 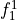 or
or 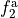 , respectively.
, respectively.
Other functional forms¶
Surkus-polynomial expansion Surkus (BobLeroy)¶
(alias BobLeroy)
![V(r) = (1-y_p^{\textrm{eq}}) \sum_{i\ge 0} a_i [y_p^{\textrm{eq}}]^i + y_p^{\textrm{eq}} a_{\rm inf},](_images/math/83826b9b89dd29cb2e438644e995598e017675a5.png)
where 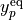 is the Surkus variable with
is the Surkus variable with 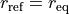
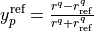
and 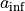 is the asymptote of the potential at
is the asymptote of the potential at 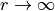 .
.
See also Eq.(36) in R. Le Roy, JQSRT 186, 167 (2017)
Example:
Bob-Rot 1 1
name "<a2Pi|BR|a2Pi>"
spin 0.5 0.5
lambda 1 1
type BOBLEROY
factor 1.0 (0, 1 or i)
values
re 0.17700000000000E+01
rref -0.10000000000000E+01
P 0.20000000000000E+01
NT 0.30000000000000E+01
a0 -0.63452015232176E+02
a1 -0.20566444179565E+01
a2 -0.13784613913938E+02
a3 0.00000000000000E+00
ainf -0.56030500000000E+02
end
Surkus-damp (alias BobLeroy_damp)¶
Surkus-polynomial expansion with a damping function:
![V(r) = T_{\rm e} + \left[ (1-y_p^{\textrm{eq}}) \sum_{i\ge 0} a_i [y_p^{\textrm{eq}}]^i + y_p^{\textrm{eq}} a_{\rm inf}\right] f^{\rm damp} + t^{\rm damp} (1- f^{\rm damp}),](_images/math/02a8f15bfd613f32b66f793a34a048170ab968ef.png)
where the damping function is defined by
![f^{\rm damp} = 1-\tanh[\alpha(r-r_0)]](_images/math/848529cb5442dc203bc365886de020de38f0bc9d.png) , and
, and 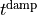 ,
, 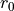 and
and 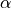 are parameters.
are parameters.
Example:
Bob-Rot 2 2
name "<a2Pi|BR|+1a2Pi>"
spin 0.5 0.5
lambda 1 1
type BOBLEROY_damp
factor 1.0 (0, 1 or i)
values
re 0.17700000000000E+01
rref -0.10000000000000E+01
P 0.20000000000000E+01
NT 0.30000000000000E+01
a0 -0.63452015232176E+02
a1 -0.20566444179565E+01
a2 -0.13784613913938E+02
a3 0.00000000000000E+00
ainf -0.56030500000000E+02
tdamp 0.00000000000000E+00
r0 0.10000000000000E+01
alpha 0.30000000000000E+01
end
POLYNOM_DIMENSIONLESS¶
This function is a polynomial
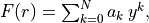 in terms of the dimensionless variable
in terms of the dimensionless variable
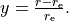
The order of the parameters in the input is as follows 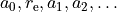
Example
dipole 1 1
name "L_2015"
type POLYNOM_DIMENSIONLESS
spin 0.0 0.0
lambda 0 0
values
re 1.12832252847d0
a0 -0.1229099d0
a1 3.604742d0
a2 -0.23716d0
a3 -3.67326d0
a4 1.4892d0
a5 1.8293d0
a6 -4.342d0
end
PADE_GOODISMAN2 (PADE2)¶
![\mu(r) = \left[P(a_i,y) + a_3/2 \right] \frac{z^3}{1+z^7}](_images/math/868bae589e5e0e43ec6aea041f584c459699b7ab.png) ,
,
where
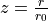 ,
,
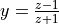 ,
,
and 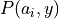 is a Tchebychev polynomial
is a Tchebychev polynomial 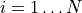 with
with 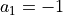 and a_2 = 1.
and a_2 = 1.
See Goodisman, J. Chem. Phys. 38, 2597 (1963).
Example:
dipole 1 1
name "<X,2Pi|DMC|X,2Pi>"
spin 0.5 0.5
lambda 1 1
factor 1 (0, 1 or i)
type PADE_GOODISMAN2
Values
RE 1.15078631518530E+00
B0 -2.36079498085387E+02 fit
B1 4.85159555273498E+02 fit
B2 -3.47080753964755E+02 fit
B3 -2.26690920882569E+02 fit
B4 -3.56214508402034E+02 fit
B5 -4.58074282025620E+02 fit
B6 -4.01237658286301E+02 fit
end
MEDVEDEV_SING2 (SING2)¶
Dipole moment function:
![\mu(r) = \frac{\left[1-\exp(-r \alpha)\right]^n}{\sqrt{\left(r^2-r_1^2\right)^2+b_1^2} \sqrt{\left(r^2-r_2^2\right)^2+b_2^2}}\sum_{i=0}^kc_i\left(1-2e^{- r\beta}\right)^i](_images/math/bdddea1c1f638e9e9824a315b50381bfc8cd7cb5.png) .
.
Example:
dipole 1 1
name "<X1Sigma+|dmz|X1Sigma+>"
spin 0 0
lambda 0 0
type MEDVDEDEV_SING2
values
alpha 0.528882306544608771D+00
beta 0.174842312392832677D+01
r1 0.367394402167278311D+00
b1 0.126545114816554061D+00
r2 0.226658916500257268D+01
b2 0.263188285464316518D+01
n 5
c0 0.954686180104024606D+04
c1 -0.100829376358086127D+06
c2 0.343009094395974884D+06
c3 -0.593296257373294560D+06
c4 0.574050119444558513D+06
c5 -0.296914092409155215D+06
c6 0.644340312384712088D+05
end
Mass-dependent BOB non-adiabatic Surkus-polynomial expansion BOBNA¶
BOB-correction.
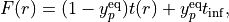
where 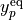 is the Surkus variable,
is the Surkus variable, 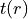 is given by
is given by
![t(r) = \mu_a \sum_{i\geq 0} a_i [y_p^{\textrm{eq}}]^i + \mu_b \sum_{i\geq 0} b_i [y_p^{\textrm{eq}}]^i](_images/math/34bb2c7ddb78e3adb2dbb67faaf9cbbc73ebdb7f.png) ,
,
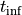 is the asymptote of the potential at
is the asymptote of the potential at 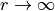 as given by
as given by
:math:`t_{rm inf} = mu_a a_{rm inf} + mu_b b_{rm inf} `.
The mass-dependent factors are given by
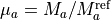
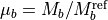
where 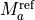 and
and 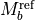 are the reference masses of the parent isotopologue.
are the reference masses of the parent isotopologue.
Example:
Bob-Rot 1 1
name "<a2Pi|BR|a2Pi>"
spin 0.5 0.5
lambda 1 1
type BOBNA
factor 1.0 (0, 1 or i)
values
re 0.17700000000000E+01
Maref 1.0000
Ma 1.0000
Mbref 12.000
Mb 12.000
P 0.20000000000000E+01
NTa 0.30000000000000E+01
NTb 0.30000000000000E+01
a0 -0.63452015232176E+02
a1 -0.20566444179565E+01
a2 -0.13784613913938E+02
a3 0.00000000000000E+00
ainf -0.56030500000000E+02
b0 -0.63452015232176E+02
b1 -0.20566444179565E+01
b2 -0.13784613913938E+02
b3 0.00000000000000E+00
binf -0.56030500000000E+02
end
Diabatic/non-adiabatic couplings¶
LORENTZ¶
Alias is LORENTZIAN. A Lorentzian type function used to represent the diabatic coupling:
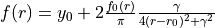 ,
,
where
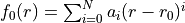
Example:
diabatic A C
name "<A|diab|C>"
lambda 1
mult 2
type Lorentz
values
V0 0.000000000000000000
RE 1.98
gamma 0.05
a0 1.58
end
LORENTZ-SURKUS¶
Alias is LORENTZIAN-SURKUS. A slightly different Lorentzian function combined with a Sukrus expansion as follows:
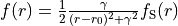 ,
,
where
![f_{\rm S}(r) = 1 + \sum_{i=1}^N a_i \left[\frac{(r^p-r_0^p)}{(r^p+r_0^p)}\right]^i.](_images/math/5967135f2a79fd217a19667f3aeea144ff0ed213.png)
Example:
diabatic A C
name "<A|diab|C>"
lambda 1
mult 2
type Lorentz-Surkus
values
gamma 0.05
RE 1.98
p 4
a1 0.1
a2 0.004
end
SQRT(LORENTZ)¶
Alais ``SQRT(LORENTZIAN)`.
A square-root of a Lorentzian type function used to represent the diabatic coupling:
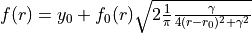 ,
,
where
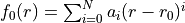
Example:
diabatic 3 5
name "<A|diab|C>"
lambda 1
mult 2
type sqrt(Lorentz)
values
V0 0.000000000000000000
RE 1.98
gamma 0.05
a0 1.58
end
Generic diabatic coupling using the angle 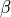 ¶
¶
As discussed above, a diabatic coupling funciton can be generated from two diabatic PECs and a transformation angle 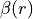 type as given by
type as given by
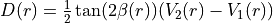 ,
,
using the COUPLED-DIABATIC, where 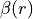 can be any function sub-type. For example:
:
can be any function sub-type. For example:
:
diabatic A C name “<A|diab|C>” lambda 1 mult 2 factor 1.0 type coupled-diabatic sub-types BETA_Lorentz factor 1.0 values gamma 2.75474715845893e-03 RE 2.02 end
is to generate a diabatic coupling generated from PEC A, PEC B (defined in the corresponding POTENTIAL sections) and a BETA_Lorentz function.
Implementation guide¶
All these analytical functions are programmed as Fortran double precision functions
in the module functions.f90.
Below is an example of a function for the EMO potential energy function.
function poten_EMO(r,parameters) result(f)
!
real(rk),intent(in) :: r ! geometry (Ang)
real(rk),intent(in) :: parameters(:) ! potential parameters
real(rk) :: y,v0,r0,de,f,rref,z,phi
integer(ik) :: k,N,p
!
v0 = parameters(1)
r0 = parameters(2)
! Note that the De is relative the absolute minimum of the ground state
De = parameters(3)-v0
!
rref = parameters(4)
!
if (rref<=0.0_rk) rref = r0
!
if (r<=rref) then
p = nint(parameters(5))
N = parameters(7)
else
p = nint(parameters(6))
N = parameters(8)
endif
!
if (size(parameters)/=8+max(parameters(7),parameters(8))+1) then
write(out,"('poten_EMO: Illegal number of parameters in EMO, check NS and NL, must be max(NS,NL)+9')")
print*,parameters(:)
stop 'poten_EMO: Illegal number of parameters, check NS and NL'
endif
!
z = (r**p-rref**p)/(r**p+rref**p)
!
phi = 0
do k=0,N
phi = phi + parameters(k+9)*z**k
enddo
!
y = 1.0_rk-exp(-phi*(r-r0))
!
f = de*y**2+v0
!
end function poten_EMO
To define a new functional form, apart from the actual function, a new reference case identifying this calculation
options needs to be added as part of the case select section in the subroutine define_analytical_field, for example:
case("EMO") ! "Expanded MorseOscillator"
!
fanalytical_field => poten_EMO