Contractions and vibrational basis set¶
Duo uses a contraction scheme to construct the rovibronic basis set used for the solution
of the coupled problem. As a first step the J=0 vibration problem is solved for each electronic state, in which the
corresponding Schroedinger equation is solved in the grid representation
of npoints. Then a certain number of the resulted
vibrational eigenfunctions  with
with 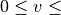 vmax and
vmax and 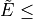
EnerMax is selected to
form the vibrational part of the basis set.
There is currently one contraction scheme supported by Duo: vibrational vib. The Omega is under construction.
The contraction type is defined in the section CONTRACTION (aliases: vibrationalbasis and vibrations)
by the keyword vib.
Vibrational contraction¶
This contraction uses a spin-free, fully uncoupled 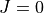 solution of the vibrational Schrödinger equation
obtained independently for each electronic state as the vibrational basis. The rovibronic basis set is then form from the Lamda-Sigma wavefunctions:
solution of the vibrational Schrödinger equation
obtained independently for each electronic state as the vibrational basis. The rovibronic basis set is then form from the Lamda-Sigma wavefunctions:
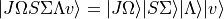
where 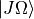 and
and  are the rigid rotor functions and
are the rigid rotor functions and 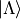 are the
electronic wavefunctions implicitly taken from the ab initio calculations.
Example :
are the
electronic wavefunctions implicitly taken from the ab initio calculations.
Example :
contraction
vib
nmax 30
enermax 25000
end
Omega (diabatic) contraction - under construciton¶
This contraction is based on a solution of vibronically coupled 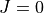 problems for each value of
problems for each value of  .
This contraction consists of two steps.
.
This contraction consists of two steps.
For each grid value of
the electronic-orbital-spin-spin-orbit coupling is diagonalised on the Sigma/Lambda basis
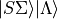 for each values of
for each values of  independently to form diabatic PECs.
independently to form diabatic PECs.
Vibrational (
) Schrödinger equations are solved for each diabatic PEC curve to obtain a Omega-vibrational basis set
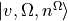 (
(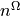 is a manyfold count within the same value of
is a manyfold count within the same value of 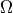 ).
).
The rovibronic basis set in the Omega representation is given by
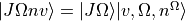
where 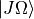 are the rigid rotor functions.
are the rigid rotor functions.
Example 2:
contraction
omega
nmax 30 10 10
end
Keywords¶
vib and omega: contraction types
nmax
(alias: vmax, vibmax) specifies the value of the maximum vibrational functions to be computed and kept for
the solution of the coupled problem. For example
nmax 15
specifies to compute for each PEC the lowest-energy 15 vibrational levels; it is also possible to specify different values of texttt{vmax} for each PEC, in which case the values must be given as a list; for example
nmax 10 15 8
specifies that for the PEC identified as poten 1 Duo should take 10 lowest vibrational states nmax=10, for
poten 2, nmax=15 and for poten 3, nmax=8.
If there are more PEC (poten 4 etc.) they will use for nmax the last value specified (nmax=8 in this example).
enermax
Alternatively or complementary to nmax one can select the vibrational energy levels to compute
by specifying an upper energy threshold (in cm-1). Similarly to nmax, one can specify a different value of enermax
for each PEC by writing a list of values; for example
enermax 30000.0 25000.0
selects a threshold of 30000 cm-1 for poten 1 and one of 25000 cm-1 for poten 2 and any other potential present.
Note that by default Duo will shift the PECs so that the lowest point of the lowest-lying PEC has zero energy, and that the energy
used for the enermax threshold are total vibrational energies including the zero point energy.
One can prevent Duo from shifting the PECs by writing in the input (anywhere but not within an input section)
the option do_not_shift_pecs.
If both enermax and vmax are specified only levels which satisfy both criteria are kept for the solution of the coupled problem.
If neither of them is specified (or the vibrationalbasis input section is missing altogether) then vmax
is taken equal to npoints for all PECs and there is a hard-coded limit of 10 8 cm-1 for enermax.
end{itemize}